Dynamic Programming이란?
- 큰 문제를 작은문제로 나누어 푸는 문제를 일컫는 말. Dynamic Programming이란 말 때문에 어떤 부분에서 동적으로 프로그래밍이 이루어지는 찾아볼 필요는 없다. 바로 동적프로그래밍이란 말을 창조한 사람도 이것이 단지 멋있어서 부여한 이름이라고 한다.
- 메모이제이션 기법을 사용한다. 그것이 핵심이다.
Dynamic Programming 방법
- 모든 작은 문제들은 한번만 풀어야 한다. 따라서 정답을 구한 작은 문제를 어딘가에 저장해 두어야 한다. 다시 그보다 큰 문제를 풀어나갈 때 똑같은 작은 문제가 나타나면 앞서 저장한 작은 문제의 결과값을 이용한다.
Dynamic Programming의 조건
- 작은 문제가 반복이 일어나는 경우.
- 같은 문제는 구할 때마다 정답이 같다.
- 위 와같은 조건을 만족하는 경우에만 동적프로그래밍을 사용할 수 있다. 작은 문제의 결과 값이 항상 같다는 점을 이용해서 큰문제를 해결하는 방법이기 때문.
예시 문제 (피보나치 수열)
- 피보나치 수열을 해결하는 전통적인 방법에는 재귀함수 호출을 통해 해결할 수 있다.
- 피보나치는 1,1,2,3,5,8, ...의 수를 이룬다. 즉, 다음 수열 = 이전 수열 + 두단계 전 수열의 합이라는 식을 갖게 된다.
- 재귀 함수로 풀게되면 간단하게 풀 수 있지만 n이 증가함에 따라 호출되는 함수가 기하급수 적으로 증가하기 때문에 일정 수 이상의 수열을 구하기 어렵다.
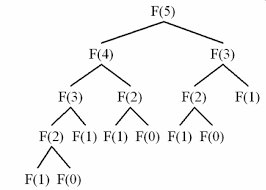
재귀 함수를 통한 피보나치 수열
- fibonacci를 재귀함수로 풀게될 경우, 위의 그림처럼 했던 작업을 또 하게 된다. 이럴 때 DP의 조건두가지를 상기해보면 이를 동적계획법을 이용해 풀 수 있다는 사실을 알 수 있다.
- 작은 문제들이 반복된다.
- F(5)를 구하기 위해서는 F(4), F(3)이 필요하다. 다시 F(4)를 구하기 위해서는 F(3),F(2)가 필요하다. 이 경우를 살펴보면 F(5)에서도 F(3)이 필요하고 F(4)에서도 F(3)이 필요함을 알 수 있다. 즉, 작은 문제가 반복되는 구조이다.
- 같은 문제는 구할때 마다 정답이 같다.
- Fibonacci 수열의 경우 첫번째 두번째 수열은 각각 1로 고정되어 있다. 즉, 3번째 수열은 언제나 결과가 2이다. 또 4번째 수열은 3번째 수열과 2번째 수열을 이용해 구하므로 언제나 정답이 같다는 사실을 알 수 있다.
DP의 첫번째 방식
int save[100];
int DP(int x)
{
if (x == 1) return 1;
if (x == 2) return 1;
if (save[x] != 0) return save[x];
return save[x] = DP(x - 1) + DP(x + 1);
}
처음 만난 문제가 아니면, 즉, 기존에 만나서 저장했던 문제라면 기존에 풀고 저장해뒀던 것을 불러오기만 하면 된다.
처음 만난 문제라면 계산 해서 구한다.
위 부터 계산해 내려가는 방식이기 때문에 Top - Down 방식이라고 부른다.
DP 두 번째 방법
int save[100];
int DP(int x)
{
save[0] = 0; save[1] = 1;
for(int i = 2; i <= n; i++)
save[i] = save[i - 1] + save[i - 2];
return save[x];
}
재귀 안 쓰고 반복문으로 처음부터 저장해나간다.
아래 부터 계산해 올라가는 Bottom - Up 방식이다.
출처
https://ansohxxn.github.io/algorithm/dp/
(C++) 동적 계획법 Dynamic Programming
나동빈님 블로그 참고함
ansohxxn.github.io
https://galid1.tistory.com/507
알고리즘 - Dynamic Programming(동적프로그래밍)이란?
Dynamic Programming(동적계획법) 이란 1. Dynamic Programming(동적계획법)이란?큰 문제를 작은문제로 나누어 푸는 문제를 일컫는 말입니다. 동적 계획법이란 말 때문에 어떤 부분에서 동적으로 프로그래밍
galid1.tistory.com
'C++ STL, 알고리즘' 카테고리의 다른 글
| c++ static (0) | 2024.10.02 |
|---|---|
| c++ 복습을 위한 링크 (0) | 2024.08.30 |
| Greedy와 DP 알고리즘에 대한 고찰 (0) | 2023.11.22 |
| BFS, DFS 활용 문제 고찰 (0) | 2023.11.01 |
| c++ memset (0) | 2023.10.24 |